
Modelliertes Ende
Wie wir in diesem Jahr festgestellt haben, wächst die Anzahl der Caches trotz sinkender Publishzahlen weiter. Das ist zunächst einmal nur ein Fakt, der eigentlich keine besondere Relevanz hat. Für Neucacher ist es natürlich schön, eine hohe Anzahl auffindbarer Caches zu haben, aber was nützt es den Bestandscachern, wenn wir in der Homezone einen wachsenden Bestand von Caches haben, die wir bereits alle gefunden haben? Der steigende Cachebestand hat somit kaum praktische Relevanz, wir wollen uns heute trotzdem einmal damit auseinandersetzen, denn das Wachstum hat natürlich Grenzen. Und was danach kommen könnte, ist nicht so schön.
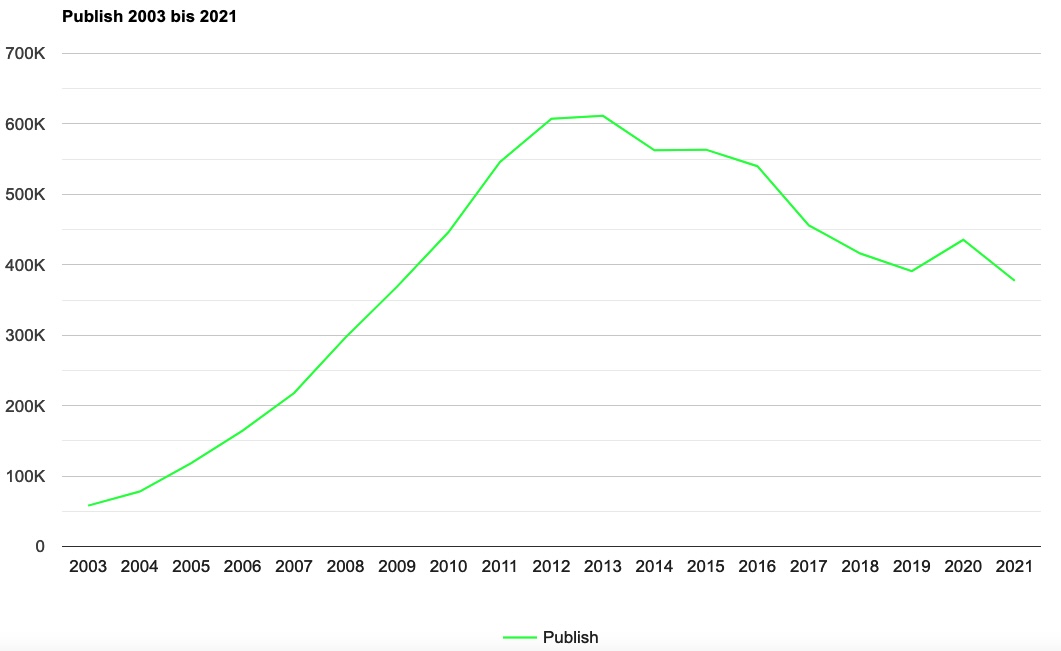
Ein paar Überlegungen dazu: Jeder Cache wird irgendwann archiviert, nach drei Monaten, einem Jahr oder einem Jahrzehnt, irgendwann ist Schluss. Stellt man sich den Verlauf der Publishzahlen als Welle vor, so folgt der Publishwelle mit einigem Abstand eine Archiverungswelle unbekannter Form. Und jetzt kommt der Teil, der bei Groundspeak für Kopzerbrechen sorgt oder sorgen sollte. Hier sind die Publishzahlen von 2003 bis 2021:
Das Maximum der Publishs war 2013, bis dahin ist die Zahl jedes Jahr gestiegen. Das heisst aber auch, dass es einen recht großen Bestand von Caches gibt, die in den nächsten Jahren archiviert werden, die Archivierungswelle steigt also in den nächsten Jahren an und wird irgendwann die Anzahl der Publishs übersteigen.
Wenn das der Fall ist, wird der Bestand an aktiven Caches erstmalig sinken.
Wann dieser Zeitpunkt ist, hängt natürlich vom Archivierungsverhalten ab. Im Folgenden habe ich drei Modellszenarien durchgespielt, die der Veranschaulichung dienen und ganz offenbar nichts mit der Realität zu tun haben.
- Modell 1: Fibonaccizahlen. Hier ist die Annahme, dass die Archivierung einer Fibonaccifolge gehorcht, das heisst: 1% der Caches wird ein Jahr nach Publish archiviert, 2% nach zwei Jahren und so weiter
- Modell 2: Reiner Zufall. In jedem Jahr nach dem Publish wird eine zufällige Prozentzahl zwischen 1 und 10 archiviert
- Modell 3: 5% pro Jahr. Von 100 Caches im Jahre X werden im Jahr X+1 5% archiviert, im Jahr X+2 ebenfalls 5% usw.
- Modell 4: 5% pro Jahr. Von 100 Caches im Jahre X werden im Jahr X+1 5% archiviert, im Jahr X+2 ebenfalls 5% usw.
| Modell | Prozente |
|---|---|
| Fibonacci | 1,2,3,5,8,13,21,34 |
| Random 1-10 | 7,3,9,6,5,9,10,3,9,8,3,10,4,6,6,2 |
| 5% pro Jahr | 5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5… |
| 1% pro Jahr | 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1… |
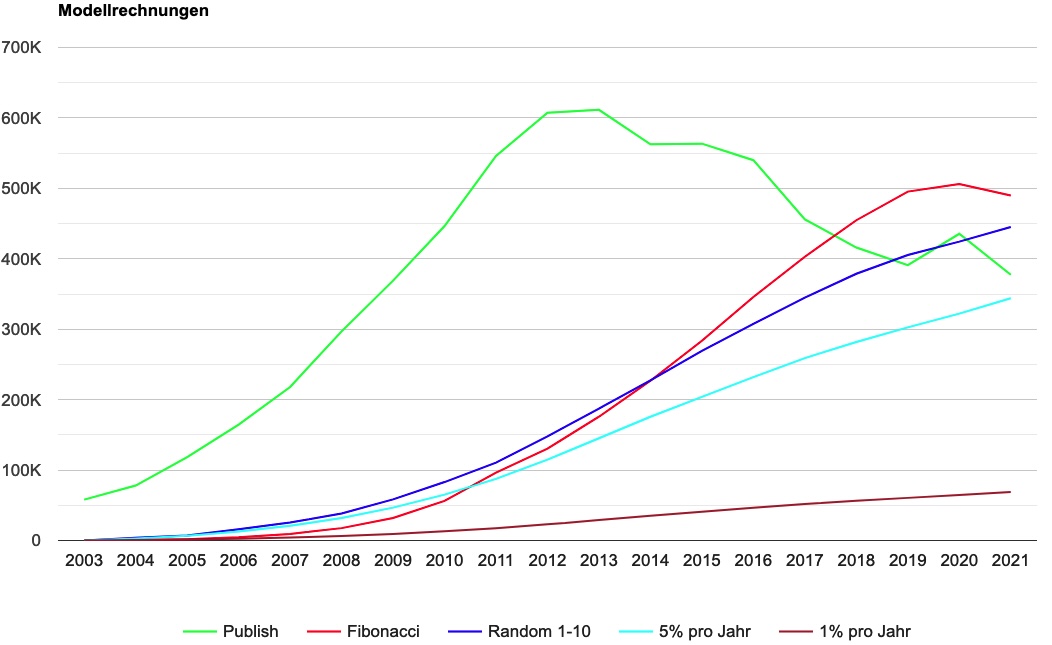
Grafisch aufbereitet sieht das so aus:
Egal welches Modell man nimmt, irgendwann überholt die Archivierungswelle die Publishwelle. Der bis 2013 aufgebaute Berg von Publishs schlägt sich mit einigem Versatz in den Archivierungszahlen nieder, selbst mit einer Rate von nur 1% ja Jahr wird die Publishzahl irgendwann übertroffen, da der hohe Bestand an aktiven Caches abgebaut wird und nicht mehr genug “Nachschub” kommt. Natürlich sinkt auch die Zahl der Archivierungen irgendwann wieder und dann gibt es zwei Szenarien:
- Die Zahl der Archivierungen sinkt schneller als die der Publishs, dann steigt der Cachebestand wieder
- Die Zahl der Archivierungen sinkt langsamer als die der Publishs, dann sinkt der Cachebestand weiter, wenn auch langsamer
Leider ist es kaum möglich, Prognosen über die zukünftige Entwicklung der Publishzahlen zu treffen.Einfach die Entwicklung von 20/21 oder 19/21(aufgrund des cornabedingten Ausreißers in 2020) als Geradengleichungen fortzuführen:
Publish20-21 = -58280 * Jahr + 118161100 Publish19-21 = -6890 * Jahr + 14301910
würde aufgrund der konstanten Steigung einfach zu bizarren Ergebnissen führen, also lassen wir es. Das war’s auch schon, vielleicht hat Euch diese kleine Zahlenspielerei ja gefallen ![]()
In diesem Sinne:
Bis bald im Wald und happy hunting
Ein Gedanke zu „Modelliertes Ende“
Kommentare sind geschlossen.